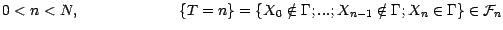Section : Le
théorème d'arrêt
Précédent : Le théorème d'arrêt
Suivant : Une
réciproque au théorème
Soit 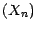 une suite adaptée à une
filtration
une suite adaptée à une
filtration
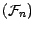 de v.a. à valeurs dans
de v.a. à valeurs dans
 et soit
et soit 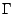 un sous
ensemble de
un sous
ensemble de  ; on pose
(avec la convention
; on pose
(avec la convention
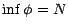 )
)
- Proposition:
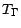 est alors un temps d'arrêt
qu'on appelle temps d'entrée de la suite
est alors un temps d'arrêt
qu'on appelle temps d'entrée de la suite 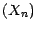 dans l'ensemble
dans l'ensemble 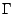
Démonstration:
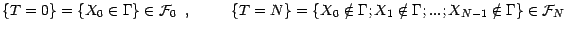
et pour
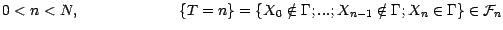
Il y a beaucoup d'autres exemples de temps d'arrêt, les plus
simples d'entre eux étant les temps d'arrêt constants.
On pourra d'autre part vérifier que la borne
inférieure, la borne supérieure et la somme de 2
temps d'arrêt sont des temps d'arrêt ; ainsi, 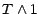 et
et 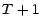 sont des temps
d'arrêt ; on réfléchira une minute au fait que
sont des temps
d'arrêt ; on réfléchira une minute au fait que
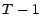 n'est pas nécessairement un temps
d'arrêt : un joueur peut décider de s'arrêter de
jouer après le premier coup qui lui a fait perdre plus de
1000 F mais il lui est malheureusement impossible de le faire
à l'instant immédiatement précédent.
n'est pas nécessairement un temps
d'arrêt : un joueur peut décider de s'arrêter de
jouer après le premier coup qui lui a fait perdre plus de
1000 F mais il lui est malheureusement impossible de le faire
à l'instant immédiatement précédent.
Jacques Azéma