Section : Temps
d'arrêt
Précédent : Définitions:
Suivant : Définition:
Soient
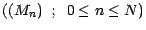 une suite de
v.a. et
une suite de
v.a. et 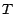 une v.a à valeurs dans
une v.a à valeurs dans
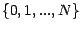 ;
;
on pose
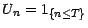 ; la transformée
de
; la transformée
de 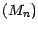 par la suite
par la suite 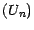 est
est

Démonstration: Il suffit de vérifier, ce qui
est facile au vu des définitions, que
Nous allons maintenant nous demander àquelle condition 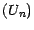 est prévisible. La réponse est
fournie par les équivalences suivantes :
On remarquera d'autre part que
est prévisible. La réponse est
fournie par les équivalences suivantes :
On remarquera d'autre part que
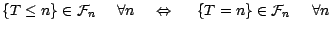
|
(3.6) |
ce qui nous conduit a la définition suivante :
Jacques Azéma