Section : Temps d'arrêt
Précédent : Temps d'arrêt
Suivant : Proposition:

Définitions:

Soit $(X_n\;\;;\;\;n\in \{0,1,2,...,N\})$ une suite de v.a. et $T$ une v.a. a valeurs dans $\{0,1,2,...,N\}$ , on notera $X_T$ la variable aléatoire définie par

$$X_T(\omega )=X_{T(\omega )}(\omega )$$

ou encore

$$X_T=\sum_{n=0}^{n=N}X_n1_{\{T=n\}}$$

et $(X^T_n)$ la suite de variables aléatoires définie par

$$X^T_n=X_n1_{\{n<T\}}+X_T1_{\{n\geq T\}}$$

ou encore

$$X^T_n=X_{n\wedge T}$$

On dira que la suite $X^T$ est la suite $X$ arrêtée a $T$ .

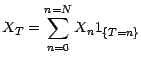
Parmi les stratégies qui s'offrent à notre joueur du paragraphe 3.3.1. , il en est une , appelée stratégie d'arrêt qui va nous intéresser maintenant ; elle consiste à miser 1F j'usqu'à un certain temps $T$ (aléatoire) puis, accès de sagesse après un gain ou bouffée dépressive après une perte, à quitter le jeu . Ce faisant, l'évolution $(M_n)$ de la fortune du joueur est remplacée par la suite $(M^T_n)$ ; cette dernière, c'est ce que nous allons voir maintenant, peut être considérée comme une transformée de $(M_n)$ .