Section : Proriétés markoviennes d'une marche
Précédent : Chaines de Markov
Suivant : Martingales
Soient 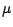 une loi de probabilité sur
une loi de probabilité sur
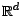 de support fini
de support fini 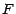 et
et
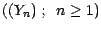 une suite de v.a.
indépendantes équidistribuées de loi
une suite de v.a.
indépendantes équidistribuées de loi 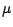 à valeurs dans
à valeurs dans
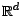 . On pose
. On pose
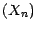 est alors une chaine de Markov de
matrice de transition
est alors une chaine de Markov de
matrice de transition
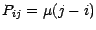
Démontrons cela ; on a , en vertu de
quand on a posé
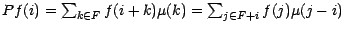 ;
on en déduit immédiatement le résultat
annoncé .
;
on en déduit immédiatement le résultat
annoncé .
Jacques Azéma
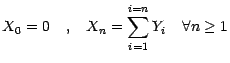
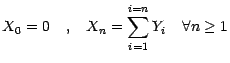
; on en déduit immédiatement le résultat annoncé .