Section : Proriétés markoviennes d'une marche
Précédent : Proriétés markoviennes d'une marche
Suivant : Matrice
de transition d'une
Revenons rapidement sur la notion de Chaine de Markov qui a
été étudiée au premier semestre . Dans
ce paragrahe , on désigera par
 un ensemble fini comportant
un ensemble fini comportant 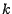 éléments que nous appellerons espace
d'états de la chaine .
éléments que nous appellerons espace
d'états de la chaine .-
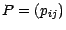 une matrice carrée
d'ordre
une matrice carrée
d'ordre 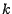 markovienne , (i.e
markovienne , (i.e
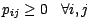 et
et
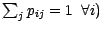 ; si
; si 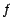 est une foncion numérique sur
est une foncion numérique sur  ,
on posera
,
on posera
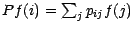
Une suite
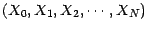 de v.a.
à valeurs dans
de v.a.
à valeurs dans  sera appelée chaine
de Markov de matrice de transition
sera appelée chaine
de Markov de matrice de transition 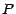 si quelque
soit la fonction numérique
si quelque
soit la fonction numérique 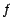 sur
sur  ,
Le lecteur vérifiera , à titre d'exercice , une
conséquence de cette égalité qui lui
rappellera peut être quelques souvenirs :
,
Le lecteur vérifiera , à titre d'exercice , une
conséquence de cette égalité qui lui
rappellera peut être quelques souvenirs :
Jacques Azéma