Section : L'espace
des épreuves
Précédent : Exemples
Suivant : Retour
aux exemples
- Une probabilité sur
 sera une
application
sera une
application
![$ \textbf{P} :\Omega \mapsto [0,1]$](img27.gif) telle que
telle que
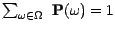
- La probabilité d'un événement
 sera définie par
sera définie par
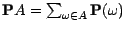
- Un couple
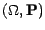 sera appelé
espace probabilisé , ou encore espace de
probabilité
sera appelé
espace probabilisé , ou encore espace de
probabilité
- l'ensemble des épreuves ayant une probabilité non
nulle est appelé support de P ; une
propriété qui est vérifiée en tout
point du support de P est dite vraie presque
sûrement (p.s.)
Si  et
et 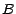 sont 2
événements , on ne dispose d'aucune formule
permettant de calculer
sont 2
événements , on ne dispose d'aucune formule
permettant de calculer
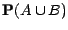 ou
ou
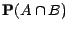 ; en revanche , si
; en revanche , si  et
et 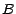 sont disjoints , on note leur
réunion par
sont disjoints , on note leur
réunion par 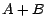 et l'on a
et l'on a
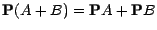 .
.
On dira que P est la probabilité uniforme sur
 si la fonction P est constante
; on a alors
si la fonction P est constante
; on a alors
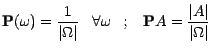
|
(1.1) |
Jacques Azéma