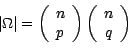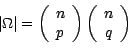Section : L'espace
des épreuves
Précédent : L'espace des épreuves
Suivant : Espaces
probabilisés
a) L'expérience aléatoire consistant en un jet
de 2 dés peut être décrite par l'ensemble
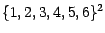 et
l'événement "la somme des deux dés a
été de 4", par le sous-ensemble
et
l'événement "la somme des deux dés a
été de 4", par le sous-ensemble
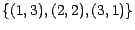
b) Dans une population  comportant
comportant  individus , on prélève au hasard pour un
sondage un échantillon de taille
individus , on prélève au hasard pour un
sondage un échantillon de taille 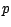 ;on pourra
prendre pour espace
;on pourra
prendre pour espace  l'ensemble
l'ensemble 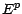 des suites
des suites
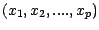 de taille
de taille 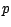 à valeurs dans
à valeurs dans  ; on a
; on a
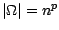 ; S'il s'agit d'un
sondage pour les élections présidentielles ,
; S'il s'agit d'un
sondage pour les élections présidentielles ,
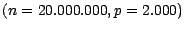 , on voit que l'espace
des épreuves , bien que restant fini , est gigantesque.
c) Cet exemple , voisin du précédent , peut
servir de modèle au jeu de loto .
, on voit que l'espace
des épreuves , bien que restant fini , est gigantesque.
c) Cet exemple , voisin du précédent , peut
servir de modèle au jeu de loto .
Soient  et
et 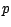 deux entiers
deux entiers 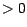 avec
avec 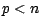 , (au loto
français ,
, (au loto
français ,
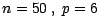 ) ; une épreuve sera un
sous ensemble de cardinal
) ; une épreuve sera un
sous ensemble de cardinal 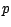 de l'ensemble
de l'ensemble
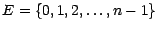 . L'espace
. L'espace  des épreuves est alors de cardinal
des épreuves est alors de cardinal
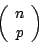
d)  est un ensemble fini de cardinal
est un ensemble fini de cardinal  ,
, 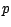 et
et 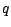 deux entiers
deux entiers 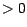 inférieurs à
inférieurs à  ; on
choisit "au hasard" deux sous ensembles
; on
choisit "au hasard" deux sous ensembles 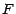 et
et 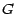 de
de  tels que
tels que 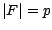 et
et 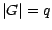 ; l'ensemble
; l'ensemble  des épreuves est
des épreuves est
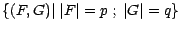 ; on a dans
ce cas
; on a dans
ce cas
Section : L'espace
des épreuves
Précédent : L'espace des épreuves
Suivant : Espaces
probabilisés
Jacques Azéma