Section : Indépendance
Précédent : Indépendance d'une famille de
Suivant : Existence et unicité en
Soient
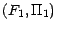 et
et
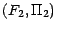 2 espaces probabilisés ;
on appellera probabilité produit de
2 espaces probabilisés ;
on appellera probabilité produit de 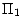 et
et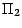 , que l'on notera
, que l'on notera
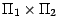 , la probabilité
, la probabilité
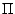 sur
sur
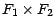 definie par
definie par
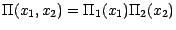 . On a
alors , si
. On a
alors , si
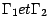 désignent
respectivement 2 sous ensembles de
désignent
respectivement 2 sous ensembles de
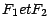 ,
,
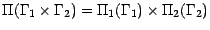
Si , maintenant ,
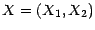 est un couple de variables
aléatoires ,
est un couple de variables
aléatoires ,
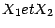 sont indépendantes si et
seulement si
sont indépendantes si et
seulement si
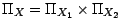 .
.
Vous constatez donc , que dans le cas d'un couple de v.a.
indépendantes , les lois marginales déterminent la
loi du couple ; mais toutes les v.a. ne sont pas
indépendantes ...
Jacques Azéma