Section : Définition :
Précédent : Définition :
Suivant : Les
prix excluant l'arbitrage
Soit 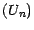 la suite des cours d'un
actif risqué
la suite des cours d'un
actif risqué 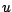
- Une option d'achat
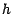 (ou call)
européenne de prix d'éxercice
(ou call)
européenne de prix d'éxercice 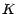 et de date d'exercice
et de date d'exercice 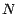 sur l'actif
sous-jacent
sur l'actif
sous-jacent 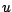 sera définie par
sera définie par
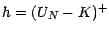 .
.
- On d'éfinit de la même façon une option
de vente
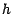 (ou put) européenne par
(ou put) européenne par
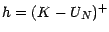 .
.
- On peut remplacer la v.a.
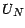 par la valeur moyenne
par la valeur moyenne
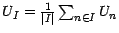 de
l'actif
de
l'actif 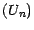 sur un intervalle de
temps
sur un intervalle de
temps
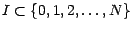 prédéterminé ; les options construites de
cette façon prennent le nom d'options asiatiques. Par
exemple un put (européen) asiatique
prédéterminé ; les options construites de
cette façon prennent le nom d'options asiatiques. Par
exemple un put (européen) asiatique 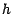 de prix
d'exercice
de prix
d'exercice 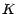 sur l'intervalle
sur l'intervalle 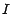 sera défini par
sera défini par
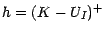 .
.
- Soient
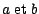 deux réels
deux réels 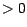 avec
avec 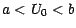 ; l'option
européenne
; l'option
européenne
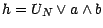 est émise par
certaines institutions financières sous le nom de
placement garanti ; un investisseur trouvant trop
risqué l'achat de l'actif
est émise par
certaines institutions financières sous le nom de
placement garanti ; un investisseur trouvant trop
risqué l'achat de l'actif 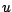 préfèrera celui de
préfèrera celui de 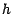 . Il sera ainsi
certain de limiter ses pertes au niveau
. Il sera ainsi
certain de limiter ses pertes au niveau 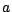 quitte
à accepter de limiter ses gains au niveau
quitte
à accepter de limiter ses gains au niveau  .
.
Jacques Azéma