Section : Marchés viables et martingales
Précédent : Marchés viables et martingales
Suivant : Options européennes
Un marché financier est viable si et seulement s'il existe
une probabilité
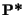 admettant
admettant  comme support sous laquelle les cours
actualisés des actifs
comme support sous laquelle les cours
actualisés des actifs
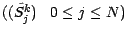 sont des
martingales.
sont des
martingales.
Démonstration : a) Supposons qu'il existe
une probabilité
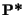 de support
de support  sous laquelle les cours actualisés des actifs
sous laquelle les cours actualisés des actifs
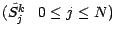 sont des
martingales. Soit
sont des
martingales. Soit
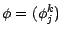 une stratégie
autofinancée telle que
une stratégie
autofinancée telle que
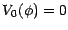 ; puisque
; puisque  est autofinancée, on a, quelque soit
est autofinancée, on a, quelque soit 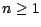 ,
,
Sous
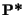 ,
,
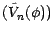 est une martingale nulle
à l'origine ; elle vérifie donc
est une martingale nulle
à l'origine ; elle vérifie donc
![$ \textbf{E*}[\tilde V_N(\phi)]=0$](img904.gif) ; il est
alors clair que
; il est
alors clair que
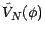 ne peut pas être une
v.a.
ne peut pas être une
v.a.  non nulle. b) Réciproquement,
supposons le marché viable ; nous allons appliquer le
théorème de Hahn-Banach dans la situation suivante
:
non nulle. b) Réciproquement,
supposons le marché viable ; nous allons appliquer le
théorème de Hahn-Banach dans la situation suivante
:
 sera l'espace euclidien des v.a.r. sur
sera l'espace euclidien des v.a.r. sur  muni du produit scalaire
muni du produit scalaire
-
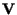 désignera le sous
ensemble de
désignera le sous
ensemble de  formé par les v.a.r.
formé par les v.a.r.
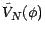 quand
quand  décrit l'ensemble
décrit l'ensemble
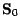 des statégies
autofinancées telles que
des statégies
autofinancées telles que
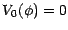 . Il est facile de voir que
. Il est facile de voir que
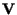 est un sous espace vectoriel de
est un sous espace vectoriel de
 .
.
- On notera
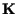 le sous ensemble de
le sous ensemble de  formé des v.a.r.
formé des v.a.r.  positives
vérifiant
positives
vérifiant
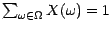 ; nous
laissons au lecteur le soin de vérifier que
; nous
laissons au lecteur le soin de vérifier que
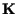 est convexe et compact. On
remarquera qu'une v.a.
est convexe et compact. On
remarquera qu'une v.a.  de
de
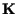 vérifie
vérifie
![$ [X>0]\not= \phi$](img913.gif) ; puisqu'il n'existe pas
de stratégie d'arbitrage,
; puisqu'il n'existe pas
de stratégie d'arbitrage,
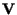 et
et
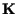 sont disjoints.
sont disjoints.
Appliquons alors le théorème de
Hahn-Banach à
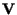 et
et
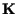 : il existe une v.a.r.
: il existe une v.a.r. 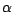 telle que
telle que
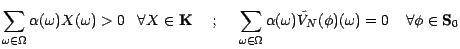
|
(4.13) |
On notera que la première
inégalité entraine
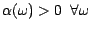 (considérer les v.a.
(considérer les v.a.  qui sont les
indicateurs des points). Posons alors
qui sont les
indicateurs des points). Posons alors
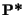 est une probabilité
chargeant tous les points de
est une probabilité
chargeant tous les points de  ; avec cette
notation la deuxième égalité de (4.13)
s'écrit
; avec cette
notation la deuxième égalité de (4.13)
s'écrit
![$\displaystyle \textbf {E*}[\tilde V_{N}(\phi)Â¥]=0\;\;\;\;\forall \phi \in \textbf {S}_{0}\; .$](img917.gif)
|
(4.14) |
Nous allons montrer que
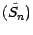 est une martingale sous
est une martingale sous
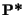 en utilisant la
caractérisation 3.4.2 ; à cet effet, donnons
nous une suite vectorielle prévisible
en utilisant la
caractérisation 3.4.2 ; à cet effet, donnons
nous une suite vectorielle prévisible
à valeurs dans
 et désignons par
et désignons par
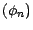 , la stratégie
de
, la stratégie
de
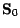 associée
à
associée
à 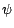 en application du
théorème 4.2.2 (avec
en application du
théorème 4.2.2 (avec
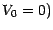 . Notons
. Notons
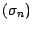 la suite
vectorielle,
la suite
vectorielle,
à valeurs dans
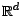 des actifs risqués
actualisés et
des actifs risqués
actualisés et
![$ [\;\;,\;\;]$](img925.gif) le produit scalaire usuel dans
le produit scalaire usuel dans
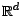 . Un calcul simple conduit
à l'égalité
. Un calcul simple conduit
à l'égalité
Prenons l'espérance des 2 membres sous
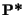 ; il vient, compte tenu de
(4.14),
; il vient, compte tenu de
(4.14),
![$ \textbf {E*}[(\psi*\sigma)_{N}]=\textbf {E*}[\psi_{0}\;,\;\sigma_{0}]$](img927.gif) ce qui montre, (Cf.3.4.2.), que
ce qui montre, (Cf.3.4.2.), que
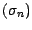 est une
P*-
est une
P*-
martingale . Il reste à remarquer que l'actif sans risque
actualisé
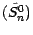 est une martingale
triviale.
est une martingale
triviale.
Section : Marchés viables et martingales
Précédent : Marchés viables et martingales
Suivant : Options européennes
Jacques Azéma
de support
sous laquelle les cours actualisés des actifs
sont des martingales. Soit
une stratégie autofinancée telle que
; puisque
est autofinancée, on a, quelque soit
,
de support
sous laquelle les cours actualisés des actifs
sont des martingales. Soit
une stratégie autofinancée telle que
; puisque
est autofinancée, on a, quelque soit
,
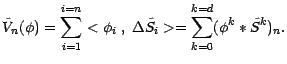
,
est une martingale nulle à l'origine ; elle vérifie donc
; il est alors clair que
ne peut pas être une v.a.
non nulle. b) Réciproquement, supposons le marché viable ; nous allons appliquer le théorème de Hahn-Banach dans la situation suivante :
et
: il existe une v.a.r.
telle que
(considérer les v.a.
qui sont les indicateurs des points). Posons alors
est une probabilité chargeant tous les points de
; avec cette notation la deuxième égalité de (4.13) s'écrit
est une martingale sous
en utilisant la caractérisation 3.4.2 ; à cet effet, donnons nous une suite vectorielle prévisible
et désignons par
, la stratégie de
associée à
en application du théorème 4.2.2 (avec
. Notons
la suite vectorielle,
des actifs risqués actualisés et
le produit scalaire usuel dans
. Un calcul simple conduit à l'égalité
; il vient, compte tenu de (4.14),
ce qui montre, (Cf.3.4.2.), que
est une P*-
est une martingale triviale.