Section : Introduction
Précédent : Introduction
Suivant : Définitions :
- Une série temporelle ou série
chronologique est une famille
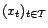 d'éléments
d'un
d'éléments
d'un
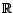 -espace vectoriel
-espace vectoriel 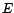 indicés par un ensemble de temps
indicés par un ensemble de temps 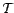 . Si
. Si
 , la série est dite
univariée ; si
, la série est dite
univariée ; si
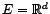 , avec
, avec 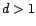 ,
elle est dite multivariée. Si
,
elle est dite multivariée. Si
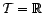 ,
,
 ,
, ![$ [a,b]$](img10.gif) , ..., on
parle de série à temps continu ; si
, ..., on
parle de série à temps continu ; si
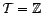 ,
,
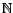 ,
,
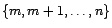 , ..., on parle de
série discrète ou à temps
discret. Sauf précision contraire, toutes les
séries étudiées dans ce cours seront
univariées et discrètes.
, ..., on parle de
série discrète ou à temps
discret. Sauf précision contraire, toutes les
séries étudiées dans ce cours seront
univariées et discrètes.
- Un processus aléatoire ou processus
stochastique est une famille
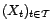 de variables
aléatoires définies sur un même espace de
probabilité
de variables
aléatoires définies sur un même espace de
probabilité
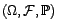 , à valeur dans
un
, à valeur dans
un
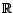 -espace vectoriel
-espace vectoriel 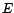 ,
et indicées par un ensemble de temps
,
et indicées par un ensemble de temps 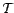 .
Si
.
Si
 , le processus est dit
réel ; si
, le processus est dit
réel ; si
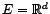 , avec
, avec 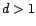 , il
est dit vectoriel. Si
, il
est dit vectoriel. Si
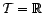 ,
,
 ,
, ![$ [a,b]$](img10.gif) , ..., on
parle de processus à temps continu ; si
, ..., on
parle de processus à temps continu ; si
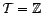 ,
,
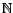 ,
,
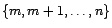 , ..., on parle de
processus discret ou à temps discret.
, ..., on parle de
processus discret ou à temps discret.
- Une trajectoire ou réalisation d'un
processus stochastique
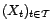 est une série
temporelle de la forme
est une série
temporelle de la forme
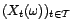 avec
avec  élément de
élément de 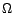 .
.
Ce cours a pour but d'apprendre à modéliser une
série temporelle par un processus stochastique, autrement
dit de déterminer un processus dont la série
temporelle soit une réalisation ``probable''. On recherchera
ce processus parmi des classes de plus en plus vastes, mais
paramètrées, de processus. Le travail de
modélisation se ramène alors à un
problème d'estimation de paramètres. Le processus
discret le plus simple et le plus fondamental est le bruit
blanc.
Section : Introduction
Précédent : Introduction
Suivant : Définitions :
Thierry Cabanal-Duvillard