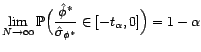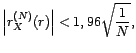 . S'il s'agit en
réalité d'un processus intégré,
c'est-à-dire si
. S'il s'agit en
réalité d'un processus intégré,
c'est-à-dire si
Supposons qu'on cherche à modéliser
![]() par un AR(1)
décentré
par un AR(1)
décentré
![]() . Si
. Si ![]() est effectivement une réalisation d'un processus
AR(1) avec
est effectivement une réalisation d'un processus
AR(1) avec
![]() , alors les
estimateurs précédemment vus sont asymptoiquement des
gaussiennes de moyenne
, alors les
estimateurs précédemment vus sont asymptoiquement des
gaussiennes de moyenne ![]() et de variance
proportionnelle à
et de variance
proportionnelle à 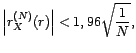 . S'il s'agit en
réalité d'un processus intégré,
c'est-à-dire si
. S'il s'agit en
réalité d'un processus intégré,
c'est-à-dire si ![]() , alors ce
résultat asymptotique n'est plus vrai. Il convient donc de
tester au préalable cette hypothèse.
, alors ce
résultat asymptotique n'est plus vrai. Il convient donc de
tester au préalable cette hypothèse.
On pose
![]() , avec
, avec
![]() . Tester H
. Tester H![]() :
: ![]() contre H
contre H![]() :
: ![]() revient à tester
revient à tester
![]() contre
contre
![]() .
.
On suppose connu le processus entre les instants ![]() et
et ![]() , et on estime les coefficients
, et on estime les coefficients ![]() et
et ![]() par une régression
linéaire ordinaire. L'estimateur
par une régression
linéaire ordinaire. L'estimateur
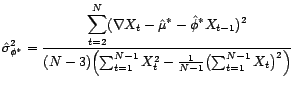 ainsi obtenu a pour variance
ainsi obtenu a pour variance