Section : Modèles SARIMA
Précédent : Exemple :
Suivant : Prévision
Soit
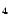 un processus du
second ordre vérifiant le modèle
SARIMA(1,1,1)(0,1,0)
un processus du
second ordre vérifiant le modèle
SARIMA(1,1,1)(0,1,0)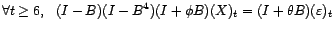 suivant :
avec
suivant :
avec
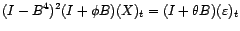 ,
et
,
et
 bruit blanc.
bruit blanc.
- Déterminer une équation de récurrence
vérifiée par la fonction moyenne du processus
 .
.
- En déduire le type de séries que l'on peut
modéliser avec ce processus.
- Mêmes questions en supposant cette fois que
 est de modèle SARIMA(1,0,1)(0,2,0)
est de modèle SARIMA(1,0,1)(0,2,0)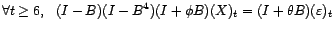 :
:
Thierry Cabanal-Duvillard