Section : Représentation causale et inversible
Précédent : Exercice 24.
Suivant : Décomposition de Wold
Soient 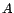 et
et 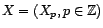 deux gaussiennes
centrées réduites,
deux gaussiennes
centrées réduites,
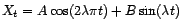 , et
, et  le processus défini par
le processus défini par
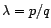 pour tout
pour tout
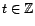 .
.
- Montrer que
 est faiblement stationnaire.
est faiblement stationnaire.
- On suppose que
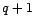 avec
avec 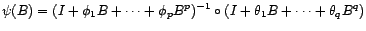 entiers irréductibles. Montrer que la fonction
d'autocorrélation partielle de
entiers irréductibles. Montrer que la fonction
d'autocorrélation partielle de  s'annule
à partir du rang
s'annule
à partir du rang 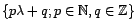 . Peut-on en
déduire que
. Peut-on en
déduire que  est un processus
auto-régressif ? Montrer qu'il s'agit d'un processus
déterministe.
est un processus
auto-régressif ? Montrer qu'il s'agit d'un processus
déterministe.
- On suppose
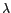 irrationnel. Alors
l'ensemble
irrationnel. Alors
l'ensemble
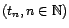 est dense dans
est dense dans
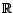 . En déduire que pour tout
. En déduire que pour tout
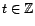 , il existe une suite
, il existe une suite
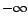 d'entiers tendant
vers
d'entiers tendant
vers 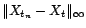 telle que
telle que
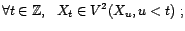 tende vers 0.
Montrer que
tende vers 0.
Montrer que  est déterministe.
est déterministe.
Thierry Cabanal-Duvillard