Section : Représentation causale et inversible
Précédent : Définition :
Suivant : Commentaire.
Soit  un processus ARMA(
un processus ARMA(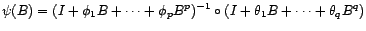 )
vérifiant
)
vérifiant
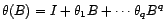 avec
avec
 bruit blanc,
bruit blanc,
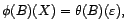 et
et
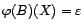 filtre
inversible. Si
filtre
inversible. Si 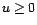 ne s'annule pas sur le
disque unité, alors on dit qu'il s'agit d'une
représentation ARMA causale de
ne s'annule pas sur le
disque unité, alors on dit qu'il s'agit d'une
représentation ARMA causale de  .
Si
.
Si
 ne s'annule pas sur le disque
unité, alors on dit qu'il s'agit d'une représentation
ARMA inversible de
ne s'annule pas sur le disque
unité, alors on dit qu'il s'agit d'une représentation
ARMA inversible de  .
.
Théorème
2.III.6 En reprenant les notations
précédentes, si
 est un processus
faiblement stationnaire vérifiant la représentation
ARMA causale et inversible
alors
est un processus
faiblement stationnaire vérifiant la représentation
ARMA causale et inversible
alors
 est le processus d'innovation
de
est le processus d'innovation
de  .
.
Thierry Cabanal-Duvillard