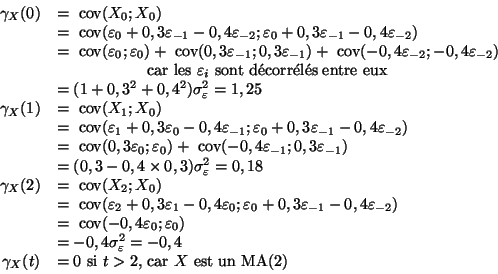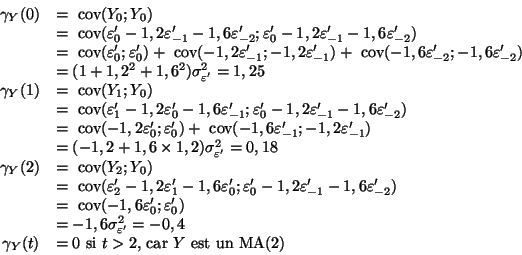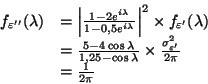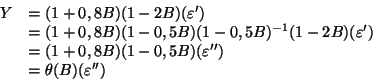Corrigé du partiel du 29 mars 2000
Statistique des processus
MST ISASH - Maîtrise MASS
Exercice 1.
Modélisation par une moyenne mobile.
Soient
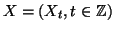 un processus stationnaire, et
un processus stationnaire, et
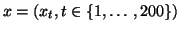 une réalisation de ce processus entre les instants
une réalisation de ce processus entre les instants 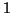 et
et 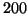 . Pour déterminer s'il est raisonnable de modéliser
. Pour déterminer s'il est raisonnable de modéliser 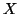 par une moyenne mobile, on utilise les deux résultats suivants :
par une moyenne mobile, on utilise les deux résultats suivants :
- L'autocorrélation empirique
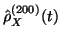 calculée sur les
calculée sur les 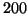 valeurs
valeurs
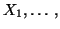
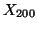 , suit approximativement une loi gaussienne de moyenne l'autocorrélation (théorique)
, suit approximativement une loi gaussienne de moyenne l'autocorrélation (théorique)
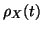 , et de variance
, et de variance 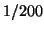 .
.
- L'autocorrélation (théorique) d'un MA(
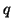 ) est nulle à partir du rang
) est nulle à partir du rang 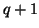 .
.
Ces deux arguments ont pour conséquence que si 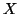 est un MA(
est un MA(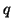 ), alors
), alors
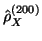 appartient à l'intervalle
appartient à l'intervalle
![$ [-1,96/\sqrt{200};1,96/\sqrt{200}]\simeq[-0,14;0,14]$](img14.gif) avec une probabilité de l'ordre de 95% pour tout
avec une probabilité de l'ordre de 95% pour tout 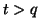 . L'autocorrélation estimée
. L'autocorrélation estimée
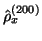 est une réalisation de l'autocorrélation empirique ; à partir du rang
est une réalisation de l'autocorrélation empirique ; à partir du rang 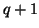 , sous l'hypothèse que
, sous l'hypothèse que 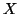 est un MA(
est un MA(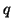 ), elle doit donc être comprise entre
), elle doit donc être comprise entre 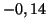 et
et 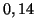 environ 19 fois sur 20. Or on constate qu'aucun phénomène de ce type n'apparaît sur l'autocorrélogramme à partir de quelque rang que ce soit.
environ 19 fois sur 20. Or on constate qu'aucun phénomène de ce type n'apparaît sur l'autocorrélogramme à partir de quelque rang que ce soit.
Une modélisation de type MA(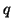 ) n'est donc pas opportune.
) n'est donc pas opportune.
Modélisation par un processus autorégressif.
On raisonne de façon tout à fait symétrique pour déterminer si une modélisation de type AR( ) est envisageable. On se sert des résultats suivants :
) est envisageable. On se sert des résultats suivants :
- L'autocorrélation partielle empirique
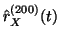 calculée sur les
calculée sur les 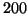 valeurs
valeurs
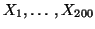 , suit approximativement une loi gaussienne de moyenne l'autocorrélation partielle (théorique)
, suit approximativement une loi gaussienne de moyenne l'autocorrélation partielle (théorique) 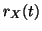 , et de variance
, et de variance 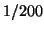 .
.
- L'autocorrélation partielle (théorique) d'un AR(
 ) est nulle à partir du rang
) est nulle à partir du rang 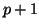 .
.
Cela a pour conséquence que si 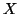 est un AR(
est un AR( ), alors
), alors
 appartient à l'intervalle
appartient à l'intervalle
![$ [-1,96/\sqrt{200};1,96/\sqrt{200}]\simeq[-0,14;0,14]$](img14.gif) avec une probabilité de l'ordre de 95% pour tout
avec une probabilité de l'ordre de 95% pour tout 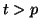 . L'autocorrélation partielle estimée
. L'autocorrélation partielle estimée
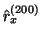 est une réalisation de l'autocorrélation partielle empirique ; à partir du rang
est une réalisation de l'autocorrélation partielle empirique ; à partir du rang 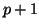 , sous l'hypothèse que
, sous l'hypothèse que 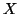 est un AR(
est un AR( ), elle doit donc être comprise entre
), elle doit donc être comprise entre 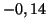 et
et 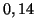 environ 19 fois sur 20. Or on constate sur l'autocorrélogramme que c'est effectivement le cas à partir de
environ 19 fois sur 20. Or on constate sur l'autocorrélogramme que c'est effectivement le cas à partir de 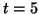 , et même, à une exception près - ce qui est acceptable sur 39 valeurs et peut correspondre aux 5% qui n'appartiennent pas à l'intervalle
, et même, à une exception près - ce qui est acceptable sur 39 valeurs et peut correspondre aux 5% qui n'appartiennent pas à l'intervalle
![$ [-0,14;0,14]$](img28.gif) -, à partir de
-, à partir de 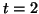 .
.
On peut donc proposer de modéliser 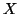 par un AR(
par un AR(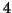 ), voire par un AR(
), voire par un AR(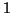 ).
).
Les équations qui permettent de déterminer les coefficients d'un modèle AR( ) sont les équations de Yule-Walker.
) sont les équations de Yule-Walker.
Hypothèse AR(1) :
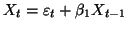 . Alors les équations de Yule-Walker se réduisent à
. Alors les équations de Yule-Walker se réduisent à
D'où l'estimation de 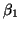 par
par
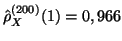 .
.
Hypothèse AR(4) :
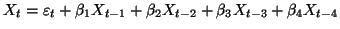 . Alors les équations de Yule-Walker deviennent
. Alors les équations de Yule-Walker deviennent
Pour estimer les coefficients
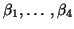 , on remplace l'autocorrélation par l'autocorrélation estimée. D'où
Remarque : ce système a pour solution
, on remplace l'autocorrélation par l'autocorrélation estimée. D'où
Remarque : ce système a pour solution
Exercice 2.
1) Montrons que 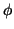 annule les composantes saisonnières.
annule les composantes saisonnières.
Méthode 1. On remarque que la transformée en 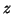 de
de 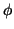 peut se décomposer en
peut se décomposer en
Autrement dit, 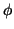 s'écrit comme produit de composition des filtres
s'écrit comme produit de composition des filtres
 ,
, 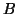 et
et
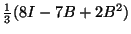 . Or
. Or 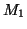 annule les composantes saisonnières de période 3. Donc
annule les composantes saisonnières de période 3. Donc 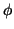 aussi.
aussi.
Méthode 2. Soit
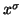 une composante saisonnière de période 3 ;
une composante saisonnière de période 3 ;
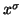 vérifie donc les propriétés suivantes :
vérifie donc les propriétés suivantes :
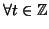 ,
,
On en déduit :
2) Montrons que 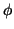 conserve les tendances polynômiales de degré inférieur ou égal à
conserve les tendances polynômiales de degré inférieur ou égal à 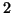 .
.
Méthode 1. Il suffit de vérifier que 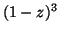 divise
divise
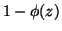 , ce qui revient à déterminer
, ce qui revient à déterminer 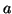 et
et 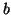 tels que
tels que
En développant, et en identifiant les coefficients, on obtient le système d'équations
Ce système admet une solution 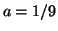 et
et 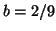 . Ce qui conclut la preuve.
. Ce qui conclut la preuve.
Méthode 2. Soit
 une tendance polynômiale quelconque de degré inférieur à 2. Montrons que
une tendance polynômiale quelconque de degré inférieur à 2. Montrons que
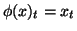 :
:
3) Le filtre 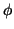 n'est pas inversible puisqu'il n'est pas injectif : toutes les composantes saisonnières de période 3 ont même image, qui est la suite nulle. En termes d'algèbre linéaire, cela signifie que le noyau de l'opérateur linéaire
n'est pas inversible puisqu'il n'est pas injectif : toutes les composantes saisonnières de période 3 ont même image, qui est la suite nulle. En termes d'algèbre linéaire, cela signifie que le noyau de l'opérateur linéaire 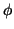 n'est pas réduit à
n'est pas réduit à 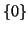 .
.
Autre preuve : 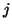 et
et 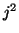 racines de
racines de 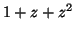 sont racines de
sont racines de 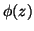 ; or elles sont de module
; or elles sont de module 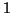 , et l'on sait qu'un filtre est inversible si et seulement si sa transformée en
, et l'on sait qu'un filtre est inversible si et seulement si sa transformée en 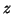 n'a pas de racine de module 1.
n'a pas de racine de module 1.
Exercice 3.
1) Il s'agit d'un modèle AR(2) (ou ARMA(2,0)), de la forme
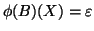 avec
avec
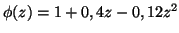 .
.
2)
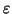 est le bruit blanc d'innovation associé à
est le bruit blanc d'innovation associé à 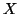 si le modèle ARMA qui détermine
si le modèle ARMA qui détermine 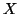 est causal et inversible. Le modèle est inversible s'il est possible d'écrire
est causal et inversible. Le modèle est inversible s'il est possible d'écrire
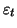 sous la forme
sous la forme
autrement comme fonction du passé de 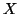 jusqu'à l'instant
jusqu'à l'instant  ; or c'est bien le cas par définition même du processus autorégressif, avec
; or c'est bien le cas par définition même du processus autorégressif, avec 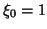 ,
,
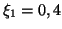 ,
,
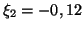 et
et 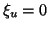 pour tout
pour tout 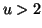 .
.
Le modèle est causal s'il est possible d'écrire 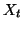 comme fonction du passé de
comme fonction du passé de
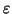 jusqu'à l'instant
jusqu'à l'instant 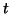 , autrement dit sous la forme
, autrement dit sous la forme
C'est le cas si et seulement si les racines de 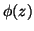 sont de module strictement plus grand que 1. Or
sont de module strictement plus grand que 1. Or
 , et ses racines sont donc
, et ses racines sont donc 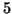 et
et 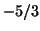 . Le modèle est donc bien causal.
. Le modèle est donc bien causal.
Conclusion :
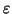 est bien le bruit blanc d'innovation associé à
est bien le bruit blanc d'innovation associé à 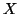 .
.
3) Soient 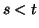 quelconques. En reprenant les notations du 2) :
quelconques. En reprenant les notations du 2) :
Comme pour tout  positif,
positif, 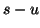 est inférieur à
est inférieur à 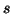 qui est strictement inférieur à
qui est strictement inférieur à 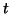 , il apparaît qu'on a toujours
, il apparaît qu'on a toujours 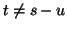 , et donc
, et donc
 (car
(car
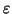 est un bruit blanc). La somme précédente est donc une somme de termes nuls, et est donc nulle. D'où
est un bruit blanc). La somme précédente est donc une somme de termes nuls, et est donc nulle. D'où
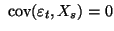 .
.
En d'autres termes,
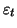 est orthogonal à son passé strict
est orthogonal à son passé strict
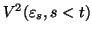 car c'est un bruit blanc ;
car c'est un bruit blanc ;
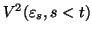 est égal à
est égal à
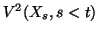 car c'est le bruit blanc d'innovation associé à
car c'est le bruit blanc d'innovation associé à 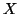 ; donc
; donc
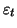 est orthogonal à
est orthogonal à 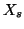 si
si 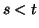 .
.
On en déduit que pour tout 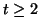 , et même
, et même 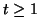 , on a
, on a
D'où l'égalité demandée.
4) Nous allons démontrer la formule par récurrence. Vérifions-la d'abord pour 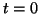 et
et 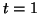 . En
. En 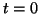 , c'est évident car
, c'est évident car
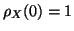 et
et
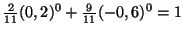 . En
. En 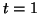 , il faut commencer par calculer
, il faut commencer par calculer
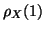 ; or, d'après la formule du 3), on a
; or, d'après la formule du 3), on a
D'où
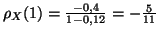 . D'autre part,
La formule est donc démontrée pour
. D'autre part,
La formule est donc démontrée pour 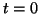 et
et 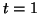 . Posons maintenant comme hypothèse de récurrence
. Posons maintenant comme hypothèse de récurrence
H(t) :
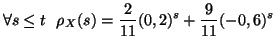
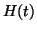 implique
implique 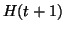 quel que soit
quel que soit 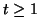 : soit
: soit 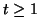 quelconque, alors
quelconque, alors
ce qui montre H(t+1). La récurrence est ainsi établie, et la formule donnant
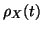 est donc vraie quelque soit
est donc vraie quelque soit 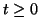 .
.
5)
Exercice 4.
1) 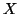 et
et 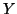 sont deux processus MA(2) (ou ARMA(0,2)) :
sont deux processus MA(2) (ou ARMA(0,2)) :
De leur nature même, ces modèles sont causals (cf exercice 3, 2)). Afin de déterminer s'ils sont inversibles, il suffit de calculer les racines des polynômes
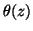 et
et
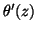 :
Les racines de
:
Les racines de
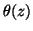 sont donc
sont donc 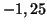 et
et 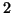 . Les racines sont de module strictement supérieur à 1, et le modèle définissant
. Les racines sont de module strictement supérieur à 1, et le modèle définissant 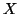 est donc inversible.
est donc inversible.
Les racines de
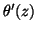 sont
sont 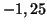 et
et 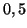 . L'une des racines est de module inférieur à 1, et le modèle définissant
. L'une des racines est de module inférieur à 1, et le modèle définissant 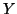 n'est donc pas inversible.
n'est donc pas inversible.
2) Fonction d'autocovariance de 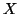 (on se servira de façon intensive du fait que
(on se servira de façon intensive du fait que
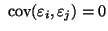 si
si 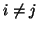 ) :
) :
Fonction d'autocovariance de 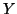 :
:
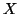 et
et 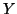 ont donc même fonction d'autocovariance. Celle-ci déterminant toutes les propriétés de second ordre du processus, il s'agit donc de deux processus ``semblables'' quoique donnés par des modèles différents. Ceci s'explique facilement en montrant qu'on peut définir
ont donc même fonction d'autocovariance. Celle-ci déterminant toutes les propriétés de second ordre du processus, il s'agit donc de deux processus ``semblables'' quoique donnés par des modèles différents. Ceci s'explique facilement en montrant qu'on peut définir 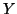 par le même modèle que
par le même modèle que 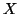 . En effet, posons
. En effet, posons
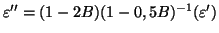 . La densité spectrale de
. La densité spectrale de
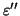 vaut :
vaut :
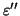 a une densité spectrale constante ; c'est donc un bruit blanc de variance
a une densité spectrale constante ; c'est donc un bruit blanc de variance
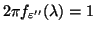 , de même variance donc que
, de même variance donc que
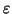 . De plus,
. De plus,
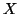 et
et 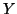 sont donc deux MA(2) qui peuvent être définis par un même modèle et associés à des bruits blancs de même variance. Rien d'étonnant à ce qu'ils aient même autocovariance.
sont donc deux MA(2) qui peuvent être définis par un même modèle et associés à des bruits blancs de même variance. Rien d'étonnant à ce qu'ils aient même autocovariance.
Thierry Cabanal-Duvillard
2001-03-21
![]() un processus stationnaire, et
un processus stationnaire, et
![]() une réalisation de ce processus entre les instants
une réalisation de ce processus entre les instants ![]() et
et ![]() . Pour déterminer s'il est raisonnable de modéliser
. Pour déterminer s'il est raisonnable de modéliser ![]() par une moyenne mobile, on utilise les deux résultats suivants :
par une moyenne mobile, on utilise les deux résultats suivants :
![]() ) n'est donc pas opportune.
) n'est donc pas opportune.
![]() ) est envisageable. On se sert des résultats suivants :
) est envisageable. On se sert des résultats suivants :
![]() par un AR(
par un AR(![]() ), voire par un AR(
), voire par un AR(![]() ).
).
![]() ) sont les équations de Yule-Walker.
) sont les équations de Yule-Walker.
![]() . Alors les équations de Yule-Walker se réduisent à
. Alors les équations de Yule-Walker se réduisent à
![]() . Alors les équations de Yule-Walker deviennent
. Alors les équations de Yule-Walker deviennent
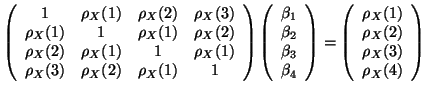

![]() annule les composantes saisonnières.
annule les composantes saisonnières.
![]() de
de ![]() peut se décomposer en
peut se décomposer en
![]() une composante saisonnière de période 3 ;
une composante saisonnière de période 3 ;
![]() vérifie donc les propriétés suivantes :
vérifie donc les propriétés suivantes :
![]() ,
,
![]() conserve les tendances polynômiales de degré inférieur ou égal à
conserve les tendances polynômiales de degré inférieur ou égal à ![]() .
.
![]() divise
divise
![]() , ce qui revient à déterminer
, ce qui revient à déterminer ![]() et
et ![]() tels que
tels que
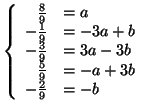
![]() une tendance polynômiale quelconque de degré inférieur à 2. Montrons que
une tendance polynômiale quelconque de degré inférieur à 2. Montrons que
![]() :
:
![]() n'est pas inversible puisqu'il n'est pas injectif : toutes les composantes saisonnières de période 3 ont même image, qui est la suite nulle. En termes d'algèbre linéaire, cela signifie que le noyau de l'opérateur linéaire
n'est pas inversible puisqu'il n'est pas injectif : toutes les composantes saisonnières de période 3 ont même image, qui est la suite nulle. En termes d'algèbre linéaire, cela signifie que le noyau de l'opérateur linéaire ![]() n'est pas réduit à
n'est pas réduit à ![]() .
.
![]() et
et ![]() racines de
racines de ![]() sont racines de
sont racines de ![]() ; or elles sont de module
; or elles sont de module ![]() , et l'on sait qu'un filtre est inversible si et seulement si sa transformée en
, et l'on sait qu'un filtre est inversible si et seulement si sa transformée en ![]() n'a pas de racine de module 1.
n'a pas de racine de module 1.
![]() avec
avec
![]() .
.
![]() est le bruit blanc d'innovation associé à
est le bruit blanc d'innovation associé à ![]() si le modèle ARMA qui détermine
si le modèle ARMA qui détermine ![]() est causal et inversible. Le modèle est inversible s'il est possible d'écrire
est causal et inversible. Le modèle est inversible s'il est possible d'écrire
![]() sous la forme
sous la forme
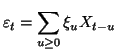
![]() comme fonction du passé de
comme fonction du passé de
![]() jusqu'à l'instant
jusqu'à l'instant ![]() , autrement dit sous la forme
, autrement dit sous la forme
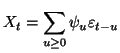
![]() est bien le bruit blanc d'innovation associé à
est bien le bruit blanc d'innovation associé à ![]() .
.
![]() quelconques. En reprenant les notations du 2) :
quelconques. En reprenant les notations du 2) :
![]() est orthogonal à son passé strict
est orthogonal à son passé strict
![]() car c'est un bruit blanc ;
car c'est un bruit blanc ;
![]() est égal à
est égal à
![]() car c'est le bruit blanc d'innovation associé à
car c'est le bruit blanc d'innovation associé à ![]() ; donc
; donc
![]() est orthogonal à
est orthogonal à ![]() si
si ![]() .
.
![]() , et même
, et même ![]() , on a
, on a
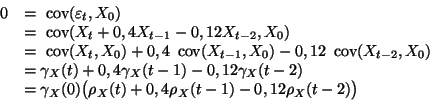
![]() et
et ![]() . En
. En ![]() , c'est évident car
, c'est évident car
![]() et
et
![]() . En
. En ![]() , il faut commencer par calculer
, il faut commencer par calculer
![]() ; or, d'après la formule du 3), on a
; or, d'après la formule du 3), on a
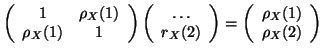
![]() et
et ![]() sont deux processus MA(2) (ou ARMA(0,2)) :
sont deux processus MA(2) (ou ARMA(0,2)) :
![]() sont
sont ![]() et
et ![]() . L'une des racines est de module inférieur à 1, et le modèle définissant
. L'une des racines est de module inférieur à 1, et le modèle définissant ![]() n'est donc pas inversible.
n'est donc pas inversible.
![]() (on se servira de façon intensive du fait que
(on se servira de façon intensive du fait que
![]() si
si ![]() ) :
) :