Section : Enveloppes de Snell et
Précédent : Enveloppes de Snell et
Suivant : Décomposition de Doob d'une
Définissons par récurrence descendante une fonction
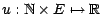 à l'aide des égalités
à l'aide des égalités
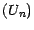 est alors égale à
est alors égale à
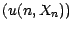 .
.
Démonstration : Elle se mène par
récurrence descendante ; si nous supposons vraie
l'égalité
on aura , en vertu de la propriété de
Markov ,
![$ \textbf{E}[U_{n+1}\vert{\cal F}_n]=Pu(n+1,.)(X_n)$](img743.gif) ,
d'où
,
d'où
Jacques Azéma
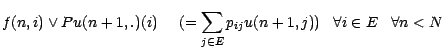
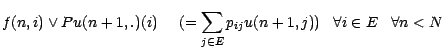
, d'où