Section : Compléments
Précédent : Compléments
Suivant : Enveloppes de Snell et
On a les égalités suivantes :
Démonstration : Appelons 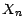 la v.a. figurant au second membre de l'
égalité (a).
la v.a. figurant au second membre de l'
égalité (a).
- Soient
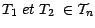 ; montrons
qu'il existe un troisième temps d'arrêt
; montrons
qu'il existe un troisième temps d'arrêt
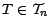 tel que
Posons pour cela
tel que
Posons pour cela
![$ A=\{\textbf{E}[Z_{T_1}\vert{\cal F}_n]\geq \textbf{E}[Z_{T_2}\vert{\cal F}_n]\}\;\;\;et\;\;T=T_11_A +T_21_{A^c}$](img719.gif) ; nous laissons au lecteur le soin de montrer que
; nous laissons au lecteur le soin de montrer que 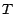 vérifie la propriété cherchée .
vérifie la propriété cherchée .
- Comme l'ensemble
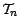 est fini , on en déduit
aisément par récurrence qu'il existe un t.a.
est fini , on en déduit
aisément par récurrence qu'il existe un t.a.
 vérifiant
vérifiant
![$ X_n=\textbf{E}[Z_{R_n}\vert{\cal F}_n]$](img721.gif) .
.
- Puisque la contante
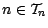 ,
,
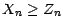 . D'autre part , on a
. D'autre part , on a
![$ \textbf{E}[X_{n+1}\vert{\cal F}_n]=\textbf{E}[Z_{R_{n+1}}\vert{\cal F}_n]\leq X_n $](img724.gif) , car
, car
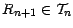 .
. 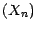 est ainsi une surmartingale majorant
est ainsi une surmartingale majorant 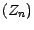 et est de ce fait
et est de ce fait
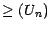 .
.
- Pour achever de montrer que
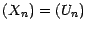 , notons que , quelque soit
, notons que , quelque soit
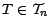 ,
,
![$ \textbf{E}[Z_T\vert{\cal F}_n]\leq \textbf{E}[U_T\vert{\cal F}_n]\leq U_n$](img728.gif) ; un passage à la borne supérieure quand
; un passage à la borne supérieure quand 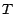 décrit
décrit
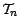 prouve alors
l'inégalité
prouve alors
l'inégalité
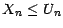 .
.
- Passons aux egalités (b) ; la remarque faite au
paragraphe précédent montre que
![$ X_n=\textbf{E}[Z_{D_n}\vert{\cal F}_n]$](img730.gif) ; de
plus , de par la définition de
; de
plus , de par la définition de 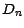 ,
,
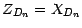 , ce qui termine la
démonstration .
, ce qui termine la
démonstration .
Jacques Azéma
![$\displaystyle (a)\hspace{0.5cm}U_n=\bigvee _{T\in {\cal T}_n} \textbf{E}[Z_T\ve... ...5cm} U_n=\textbf{E}[U_{D_n}\vert {\cal F}_n]=\textbf{E}[Z_{D_n}\vert{\cal F}_n]$](img715.gif)
![$\displaystyle (a)\hspace{0.5cm}U_n=\bigvee _{T\in {\cal T}_n} \textbf{E}[Z_T\ve... ...5cm} U_n=\textbf{E}[U_{D_n}\vert {\cal F}_n]=\textbf{E}[Z_{D_n}\vert{\cal F}_n]$](img715.gif)
la v.a. figurant au second membre de l' égalité (a).