Section : Une
réciproque au théorème
Précédent : Une réciproque au théorème
Suivant : Un
problème d'arrêt optimal
Soit
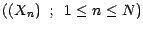 une suite
vectorielle adaptée telle que pour toute suite
prévisible vectorielle
une suite
vectorielle adaptée telle que pour toute suite
prévisible vectorielle 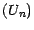 , on ait
, on ait
![$ \textbf {E}[(U*X)_{N}Â¥]=\textbf {E}[<U_{0},X_{0}>]$](img658.gif) ;
; 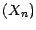 est alors une
martingale.
est alors une
martingale.
Démonstration : On se ramène
aisément au cas unidimensionnel. Si 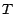 un
temps d'arrêt, la suite
un
temps d'arrêt, la suite
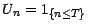 est prévisible,
et
est prévisible,
et
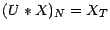 ; on a donc
; on a donc
Si  est un événement de
est un événement de
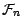 , on voit facilement
que la variable aléatoire
, on voit facilement
que la variable aléatoire
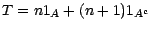 est un temps
d'arrêt, pour lequel
est un temps
d'arrêt, pour lequel
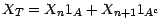 ; on peut
donc écrire
; on peut
donc écrire
On a donc
![$ \textbf {E}[X_{n}1_{A}]=\textbf {E}[X_{n+1}1_{A}]\;\;\; \forall A\in {\cal F}_{n}$](img667.gif) ; la caractérisation ( 2.3.3 ) entraîne alors
l'égalité
; la caractérisation ( 2.3.3 ) entraîne alors
l'égalité
![$ X_{n}=\textbf {E}[X_{n+1}\vert{\cal F}_{n}]$](img668.gif) ,
ce qui termine la démonstration.
,
ce qui termine la démonstration.
Jacques Azéma
un temps d'arrêt, la suite
est prévisible, et
; on a donc
est un événement de
, on voit facilement que la variable aléatoire
est un temps d'arrêt, pour lequel
; on peut donc écrire
; la caractérisation ( 2.3.3 ) entraîne alors l'égalité
, ce qui termine la démonstration.