Section : Filtrations ; suites adaptées
Précédent : Filtrations ; suites adaptées
Suivant : Martingales
- On appellera filtration sur
 une
suite croissante d'algèbres
une
suite croissante d'algèbres
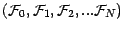 sur
sur  . Un espace probabilisé muni d'une
filtration sera appelé espace filtré
. Un espace probabilisé muni d'une
filtration sera appelé espace filtré
- On dira qu'une suite
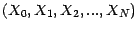 de v.a. est
adaptée à cette filtration si ,
de v.a. est
adaptée à cette filtration si ,
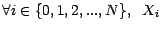 est
est
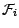 -mesurable .
-mesurable .
- On dira que cette suite est prévisible si
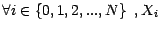 est
est
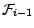 -mesurable ; (en convenant que
-mesurable ; (en convenant que
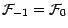 ).
).
- Soit (
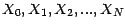 ) une suite de v.a. . On
appellera filtration naturelle engendrée par cette
suite la filtration
) une suite de v.a. . On
appellera filtration naturelle engendrée par cette
suite la filtration
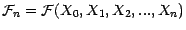 ;
(nous avons vu en 2.3.1 qu'il s'agissait bien d'une
filtration).
;
(nous avons vu en 2.3.1 qu'il s'agissait bien d'une
filtration).
La suite(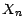 ) est adaptée a cette filtration
tandis que la suite (
) est adaptée a cette filtration
tandis que la suite (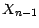 ) ,(avec la convention
) ,(avec la convention
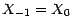 ) ,est prévisible. On peut
construire à l'aide de (
) ,est prévisible. On peut
construire à l'aide de (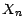 ) d'autres suites
adaptées
) d'autres suites
adaptées
intéressantes : supposons, pour simplifier, que les v.a.
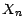 soient à valeurs dans le
même espace
soient à valeurs dans le
même espace  et donnons nous une suite (
et donnons nous une suite (
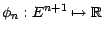 )
d'applications numériques ; pour tout
)
d'applications numériques ; pour tout  ,
la v.a.r.
,
la v.a.r.
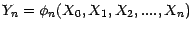 est
est
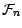 -mesurable , (elle est constante
sur chaque atome de
-mesurable , (elle est constante
sur chaque atome de
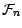 ) , de sorte que la suite
) , de sorte que la suite 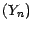 est adaptée ; dans le cas ou les v.a.
est adaptée ; dans le cas ou les v.a. 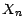 sont réelles , les suites
sont réelles , les suites
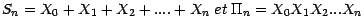 sont
ainsi des suites adaptées .
sont
ainsi des suites adaptées .
Jacques Azéma