Section : Indépendance
Précédent : Indépendance d'une famille
d'événements:
Suivant : Indépendance d'une famille de
Soient 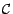 et
et 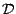 deux classes
d'événements ; on dira que
deux classes
d'événements ; on dira que 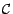 et
et
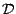 sont indépendantes si
Une v.a.
sont indépendantes si
Une v.a. 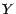 sera dite indépendante d'une classe
sera dite indépendante d'une classe
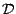 si les classes
si les classes
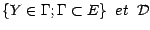 sont
indépendantes .
sont
indépendantes .
Jacques Azéma