Section : Prix et
couverture d'un
Précédent : Prix et couverture d'un
Suivant : Exercice
Soit
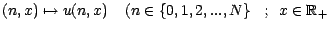 ) la suite de fonctions definie par récurrence descendante
par les égalités
Le prix
) la suite de fonctions definie par récurrence descendante
par les égalités
Le prix 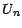 du put américain de prix
d'exercice
du put américain de prix
d'exercice 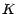 sur l'actif risqué
sur l'actif risqué 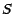 est alors
est alors
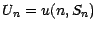 à la date
à la date 
Démonstration : On a , d'après
5.2.2 ,
![$ U_{n-1}=Z_{n-1}\vee \frac{1}{1+r}\textbf{E*}[U_n\vert {\cal F}_{n-1}]$](img1200.gif) ; raisonnons par récurrence descendante , et supposons que
; raisonnons par récurrence descendante , et supposons que
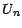 puisse s'écrire
puisse s'écrire 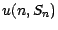 ; l'égalité précédente
devient alors
; l'égalité précédente
devient alors
Il ne reste plus qu'à appliquer la formule (13)
pour obtenir le résultat .
Jacques Azéma
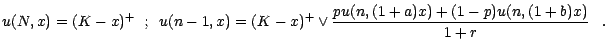
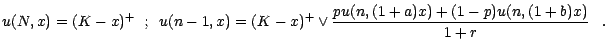
; raisonnons par récurrence descendante , et supposons que
puisse s'écrire
; l'égalité précédente devient alors