Section : Les
prix d'une option
Précédent : Les prix d'une option
Suivant : Complément
Soit 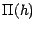 le sous ensemble de
le sous ensemble de
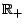 contitué par les prix excluant l'arbitrage de l'option
contitué par les prix excluant l'arbitrage de l'option 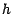 ; on a
; on a
![$\displaystyle \Pi(h)=\{\;\textbf {E*}[\tilde{h}]\;\;;\;\textbf {P*}\in \cal{P}\;\}$](img1045.gif)
|
(4.31) |
Démonstration
- Soit
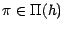 ; il existe alors une suite
adaptée
; il existe alors une suite
adaptée 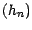 vérifiant
vérifiant
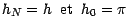 telle que le
marché
telle que le
marché
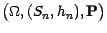 soit viable. Il existe donc (Cf.
soit viable. Il existe donc (Cf. ![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) une
probabilité
) une
probabilité
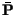 chargeant tous les points
de
chargeant tous les points
de  sous laquelle
sous laquelle
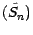 et
et
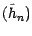 sont des
martingales ; il en résulte en particulier que
sont des
martingales ; il en résulte en particulier que
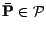 . De plus,
. De plus,
![$ \pi = h_{0}= \bar{\textbf {E}}[\tilde{h}]$](img1052.gif) ,
ce qui montre que
,
ce qui montre que 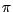 appartient au membre de
droite de (4.31).
appartient au membre de
droite de (4.31).
- Inversement, soient
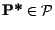 et
et
![$ \pi =\textbf {E*}[\tilde{h}]$](img1053.gif) ; posons
; posons
![$ \tilde{h}_{n}=\textbf {E*}[\tilde{h}\vert{\cal F}_{n}] =\beta_{n}Â¥ h_{n}$](img1054.gif) . Comme
. Comme
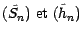 sont des
sont des
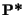 -martingales, le marché
étendu
-martingales, le marché
étendu
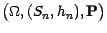 est viable ; d'autre part, on voit immédiatement que
est viable ; d'autre part, on voit immédiatement que
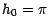 et
et 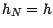 ; il en résulte que
; il en résulte que
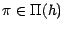 .
.
Jacques Azéma