Section : Espérance d'une variable aléatoire
Précédent : Espérance d'une variable aléatoire
Suivant : Loi
d'une variable aléatoire
Soit  une variable aléatoire à
valeurs réelles;on posera
une variable aléatoire à
valeurs réelles;on posera
![$\displaystyle \textbf{E}[X]= \sum_{\omega \in \Omega } X(\omega )\textbf{P}(\omega )$](img84.gif)
|
(1.5) |
Rappelons quelques propriétés essentielles de
l'espérance résultant imméditement de sa
définition :
- Espérance d'un indicateur : On a
![$ \textbf{E}[1_A]=\textbf{P}A$](img85.gif) quelque soit
l'événement
quelque soit
l'événement 
- Linéarité: Si
 et
et 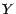 sont 2 v.a.r et si
sont 2 v.a.r et si 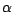 et
et 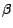 sont 2 nombres réels , on a
sont 2 nombres réels , on a
- Positivité: Si
 est positive , son
espérance est positive et n'est nulle que si
est positive , son
espérance est positive et n'est nulle que si  est presque sûrement nulle
est presque sûrement nulle
- Inegalité de convexité: Si
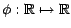 est
une fonction convexe , alors
est
une fonction convexe , alors
![$ \textbf{E}[\phi (X)]\geq \phi (\textbf{E}[X])$](img91.gif)
- Exemple: Retournons encore une fois à l'exemple
b) ; compte tenu de la remarque faite à la fin du
paragraphe précédent , on a
quand on a posé
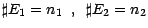
- Exercice : Soient
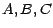 trois
événements d'un espace de probabilité
trois
événements d'un espace de probabilité  ; montrer l'égalité
Généraliser à un nombre quelconque
d'événements .
; montrer l'égalité
Généraliser à un nombre quelconque
d'événements .
Jacques Azéma
![$\displaystyle \textbf{E}[Z_1]=\sum_1^p\textbf{E}[Y_i]=\sum_1^p\textbf{P}[X_i\in E_1]=\sum_1^p{n_1\over n} = p{n_1\over n}$](img92.gif)